Previously we discussed our progress in testing some approaches to mechanistic anomaly detection (MAD). This is a short update on progress since then.
- We found anomaly detection performance was much worse for Llama 3.1 8B trained in the same way as Mistral 7B v0.1, the model that we were using previously.
- We found that Llama was somewhat less quirky than Mistral, but it still exhibited the desired quirky behaviour and achieved lower loss on average across the tasks.
- We found that the ratio of between-context variance to total variance of the hidden state activations at a given layer explained MAD performance well, and that Llama had lower variance in hidden state activations than Mistral.
- We found a weak correlation between hidden state variance and the total variance of output logits.
Overall, these results are discouraging for our MAD approaches. While Llama was less quirky than Mistral on the datasets where we found anomaly detection hard, it was still unambiguously quirky. This suggests that it’s possible for models to develop practically important anomalous behaviour without our MAD methods being able to reliably detect it.
We also tested two more approaches to anomaly detection:
- Using the outputs of a normalising flow trained on activations of hidden layers of Llama 3.1 base.
- Using the latent activations of a sparse autoencoder trained on the activations of hidden layers of Llama 3.1 base.
Both approaches yielded a performance profile remarkably close to the performance of the Mahalanobis distance on raw activations.
Anomaly detection on Llama 3.1 8B
We had previously held Llama 3.1 8B out of our experiments as a “validation model” for the MAD approaches we were testing. As we’ve reached a point where we are no longer testing a variety of MAD approaches, we decided to run our tests on Llama 3.1 8B to see how the methods performed on a different model.
For all non-arithmetic quirky datasets, we found that all of our anomaly detection methods achieved only trivial performance on Llama 3.1 8B. For the arithmetic datasets, anomaly detection methods performed similarly well to Mistral 7B v0.1.
Figure 1: Comparison of MAD AUC at different internal layers between Meta and Mistral models
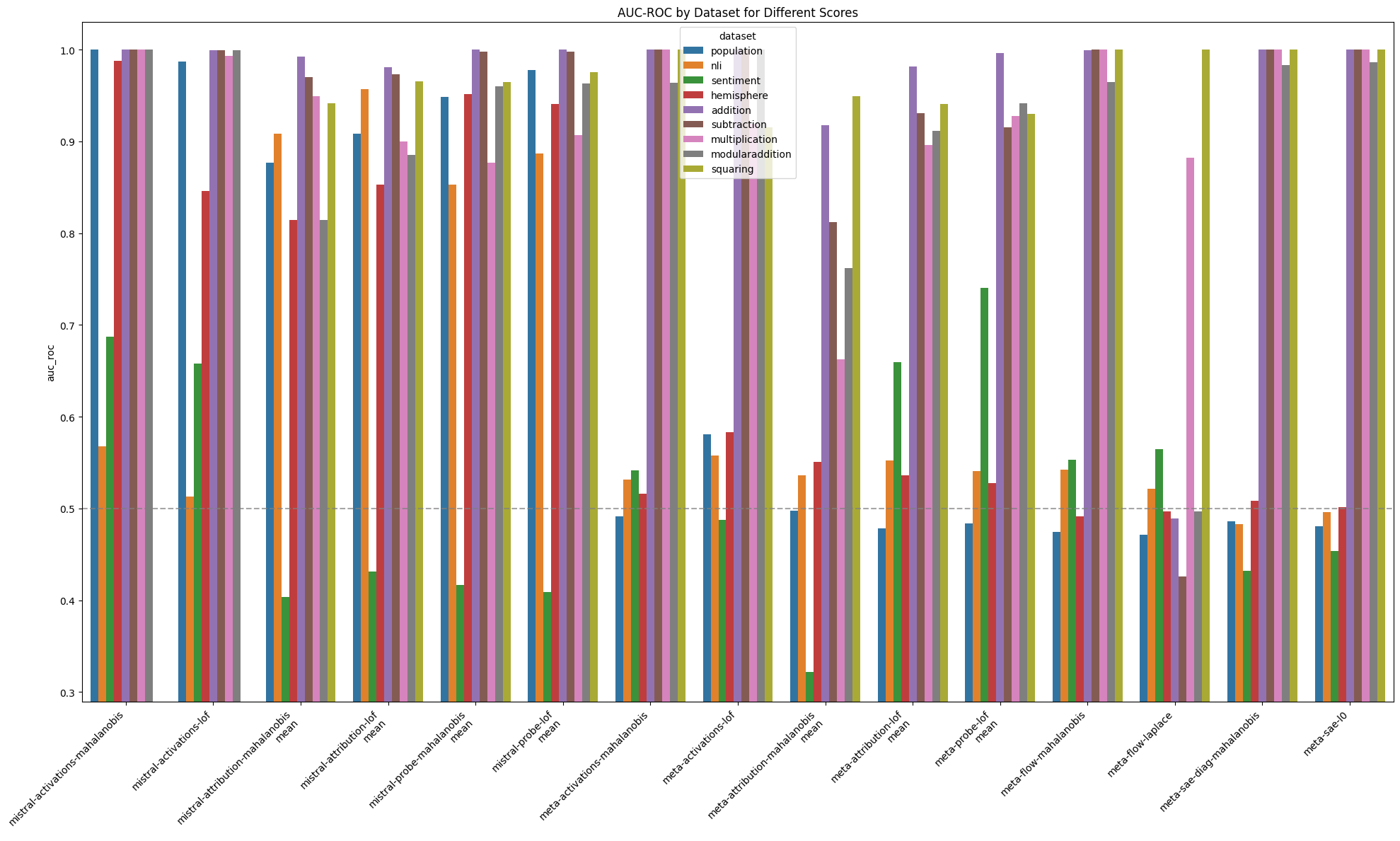
Figure 2: Comparison of MAD AUC aggeragated across internal layers between Meta and Mistral models
Llama 3.1 was less quirky than Mistral 7B v0.1
While the Llama 3.1 models exhibited quirky behaviour on most datasets, they were significantly less quirky on the non-arithmetic datasets than their Mistral 7B v0.1 counterparts. The difference seems mainly attributable to the Llama models being less confident than the Mistral models. Llama models were also somewhat more biased towards the ground truth label than Mistral models – that is, Llama’s Bob prompts give more weight to Alice’s labels than the reverse, and this bias is stronger than Mistral’s.
We fine-tuned our models until the validation loss began to rise, then selected the checkpoint with the lowest validation loss. Thus, training for longer would probably not improve the quirkiness of the Llama models (at least, not without significant performance degradation on other dimensions). It’s possible that some other modification of our fine-tuning approach could yield better model behaviour.
We did observe that attribution based methods (particularly the probe score) show substantially better performance on the sentiment dataset than activation based methods – evidence that attribution patching methods can be effective where activation based methods are not, though (as we found in our previous report) this is usually not the case.
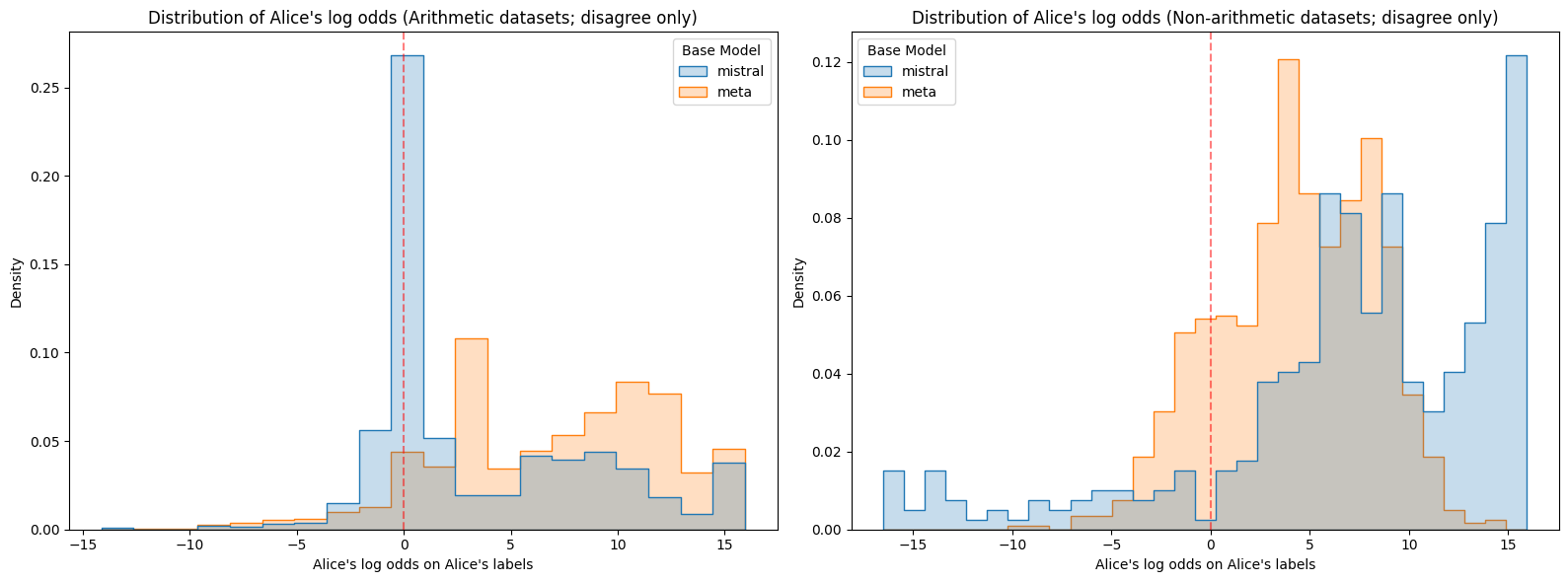
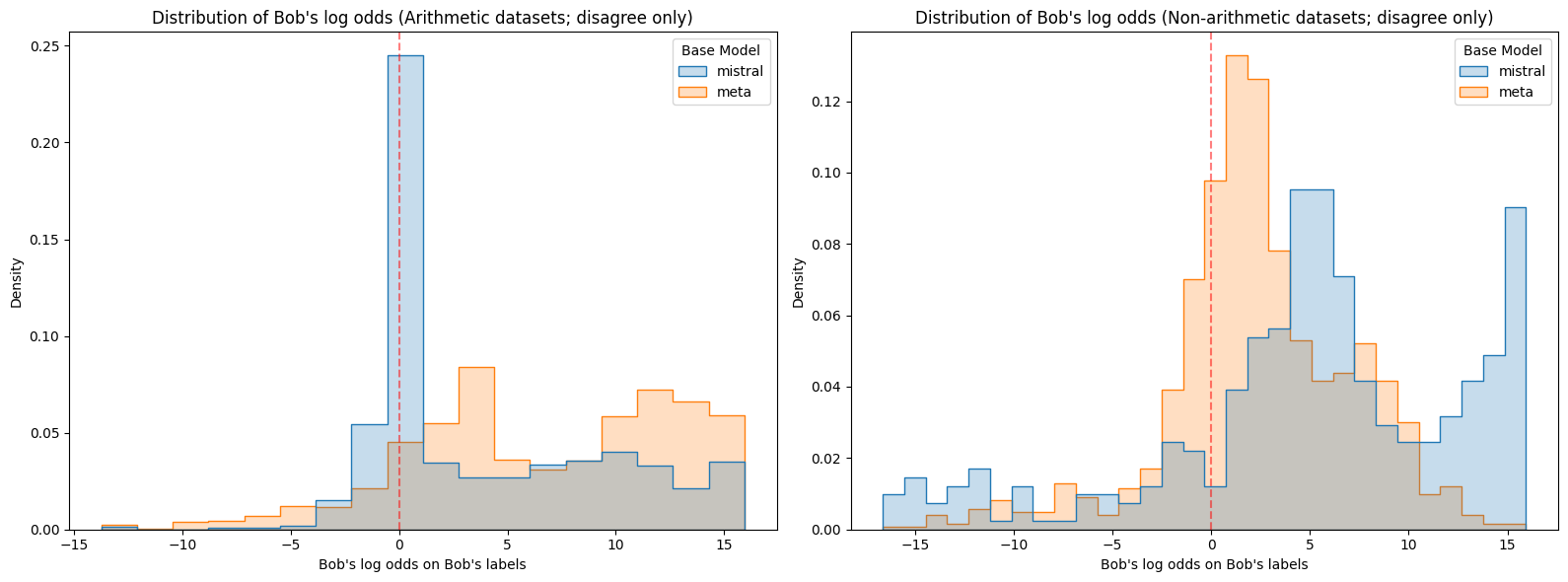
Figure 3: Log odds assigned to Alice or Bob’s labels on the corresponding prompts for each model. mistral is Mistral 7B v0.1 and meta is Meta Llama 3.1 8B. Note that Meta on non-arithmetic datasets stands out as having lower confidence than the other model-dataset combinations. On the other hand, Mistral on non-arithmetic datasets stands out as being confidently wrong with higher frequency than the other model-dataset combinations.
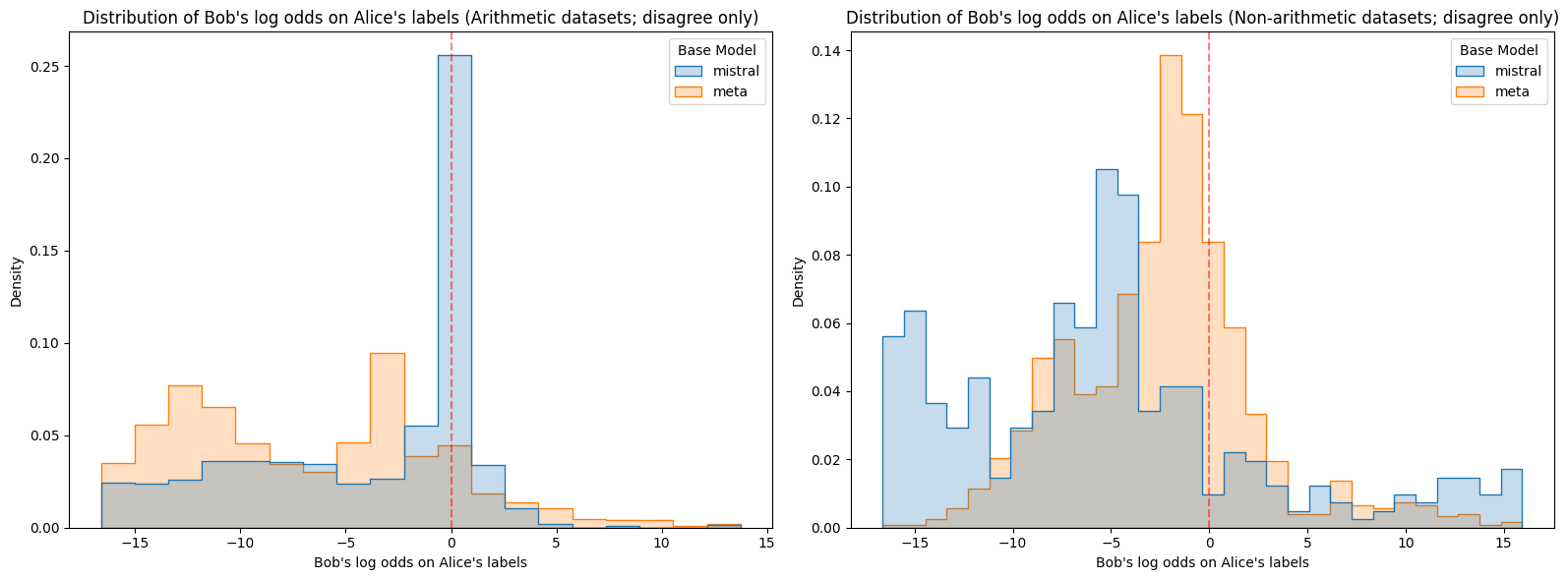
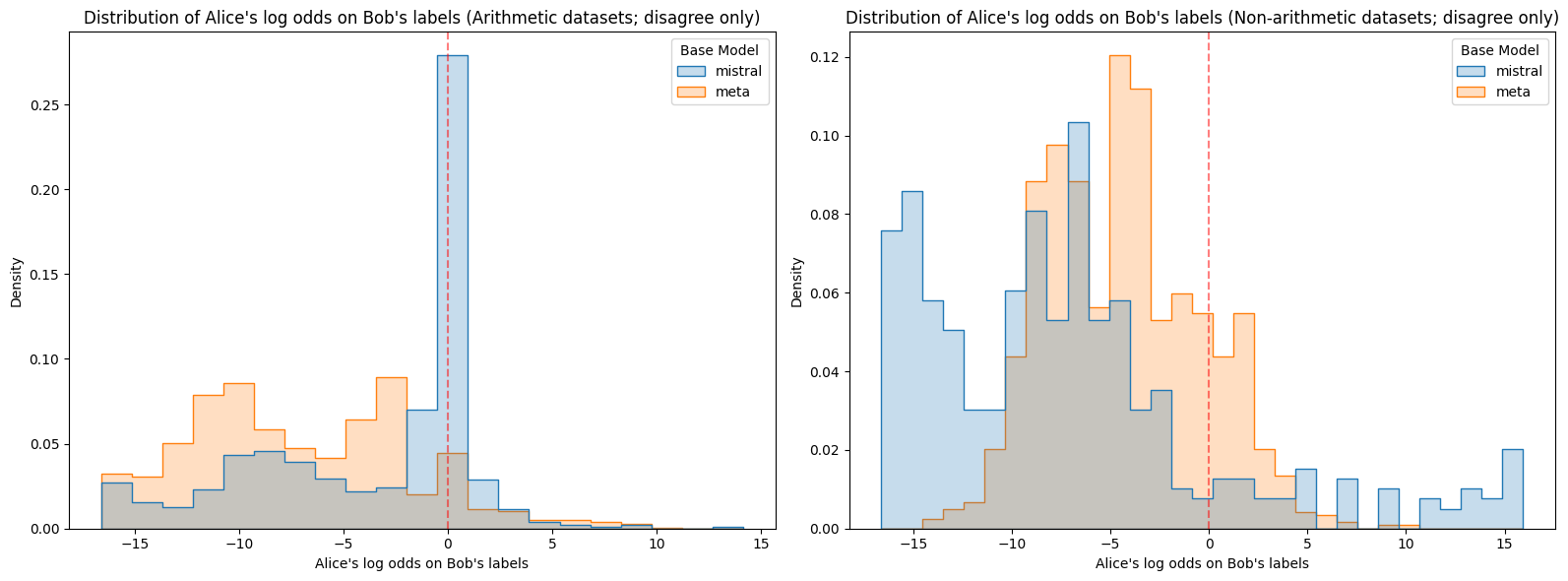
Figure 4: Log odds assigned to Alice or Bob’s labels on opposing prompts for each model. Again, Meta stands out as having lower confidence than the other model-dataset combinations, and Mistral is again unusually likely to be confidently wrong on non-arithmetic datasets.
We quantify the degree of quirkiness of a model by the shift (in logits) induced by switching labels from Alice to Bob on questions where Alice and Bob have opposing labels. We observed a significant correlation between the quirkiness of a model and the performance of the MAD methods for Llama, but less of a correlation for Mistral. This might be related to the fact that Mistral was, overall, substantially worse than Llama.
Figures 5 and 6 show the relationship between MAD AUC and “quirkiness coefficient” for each model and dataset. The quirkiness coefficient is the minimum of the difference between the loss of Alice on Bob’s labels and the loss of Alice on Alice’s labels, and the difference between the loss of Bob on Bob’s labels and the loss of Bob on Alice’s labels. If the coefficient is below 0, then at least one character does not exhibit the desired behaviour at all – note that this applied to Llama on sciq, nli and hemisphere.
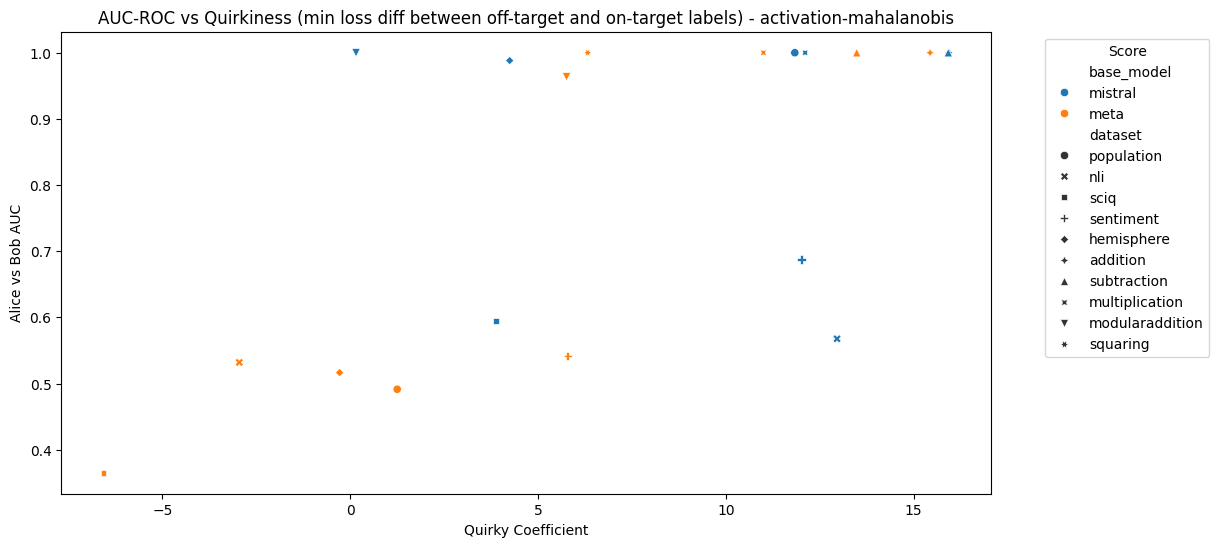
Figure 5: MAD AUC using activations and the Mahalanobis distance vs quirkiness coefficient for each model and dataset
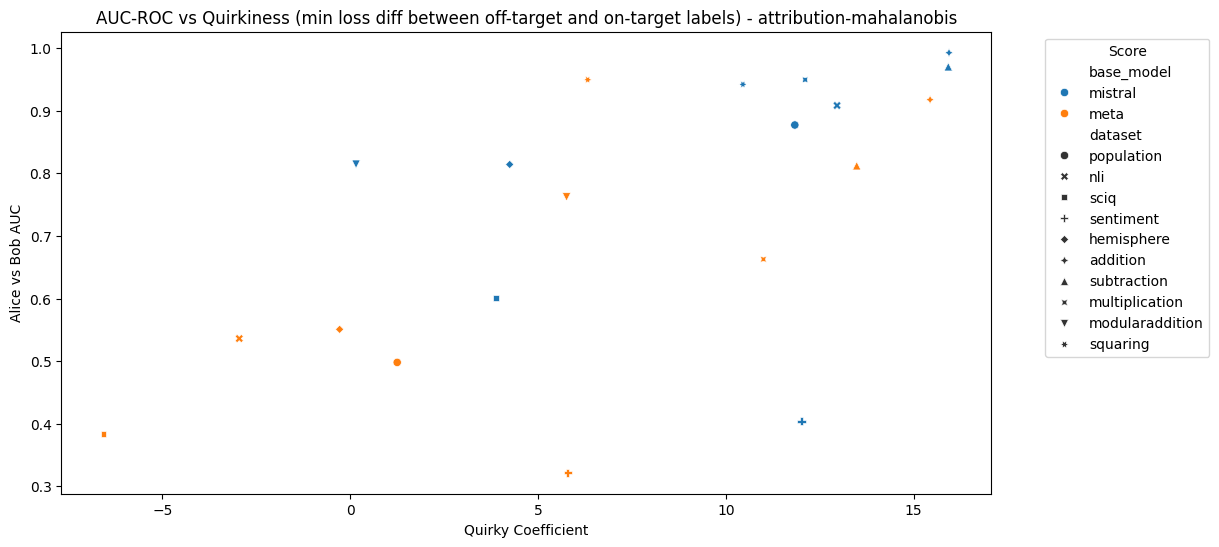
Figure 6: MAD AUC using attribution patching and the Mahalanobis distance vs quirkiness coefficient for each model and dataset
Figures 7 and 8 compare the average loss of both models against both the correct labels (i.e. Alice’s labels for Alice’s prompts) and the incorrect labels (i.e. Bob’s labels for Alice’s prompts). Llama clearly achieves lower loss on average across most datasets. Furthermore, Llama clearly achieves notably low average loss on Alice’s labels for Bob’s prompts, which is further evidence of the ground truth bias we noded in Figures 3 and 4.
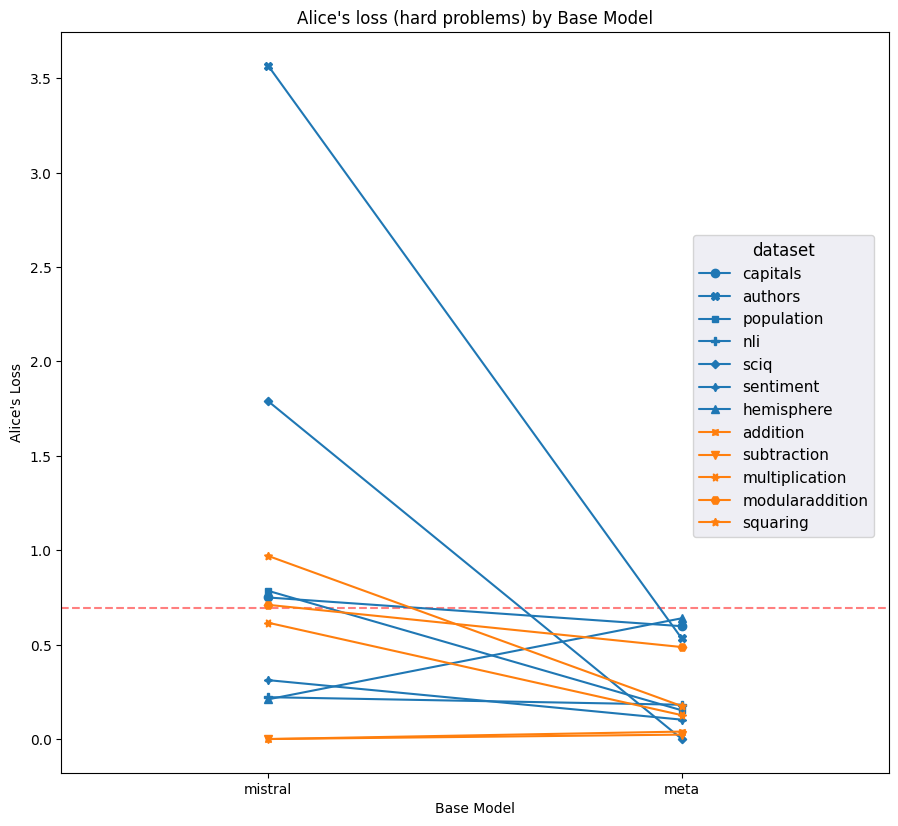
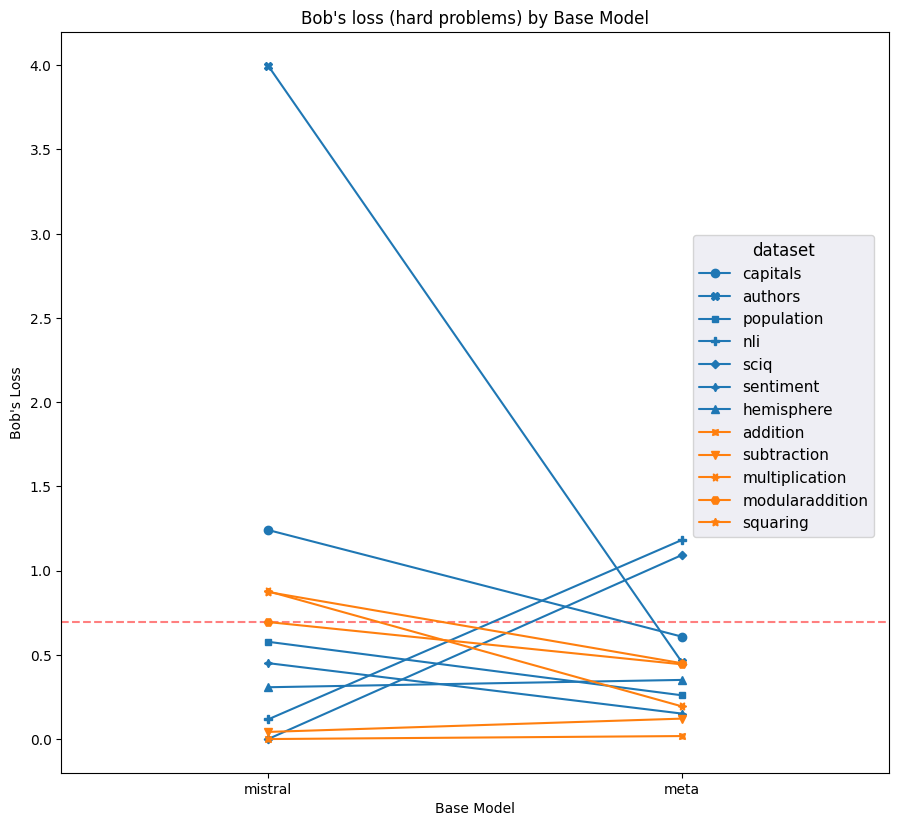
Figure 7: Averge loss on Alice’s labels on Alice’s prompts and Bob’s labels on Bob’s prompts for each model and dataset (hard examples only); lower is better. Red dashed line indicates the average loss incurred by putting 50% on each label for every question. Meta notably outperforms Mistral on most datasets.
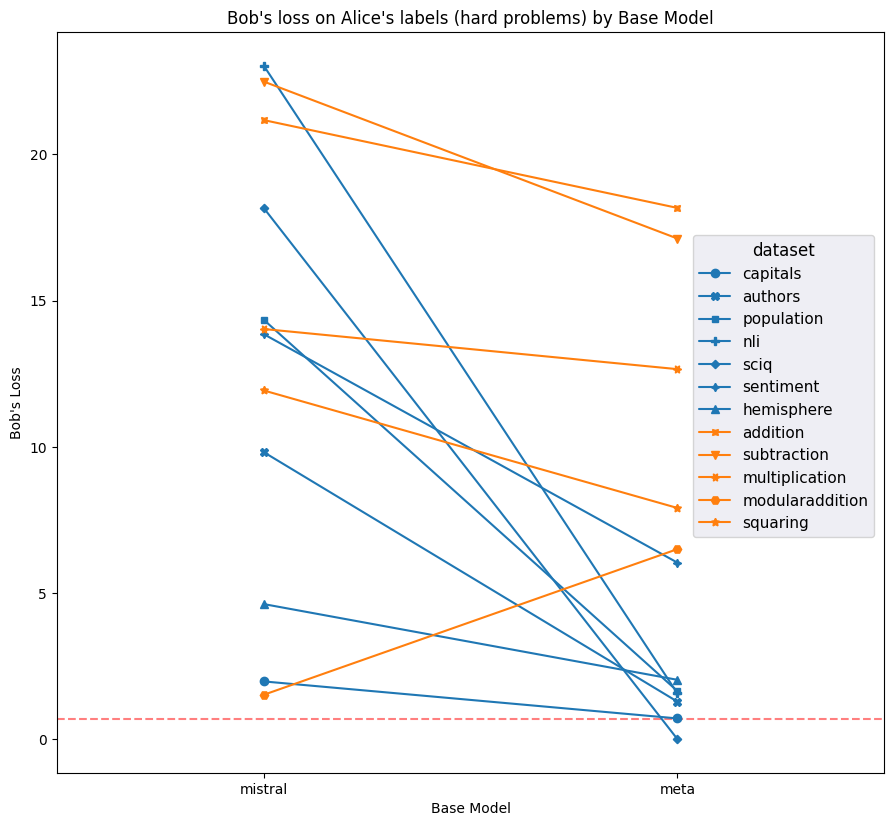
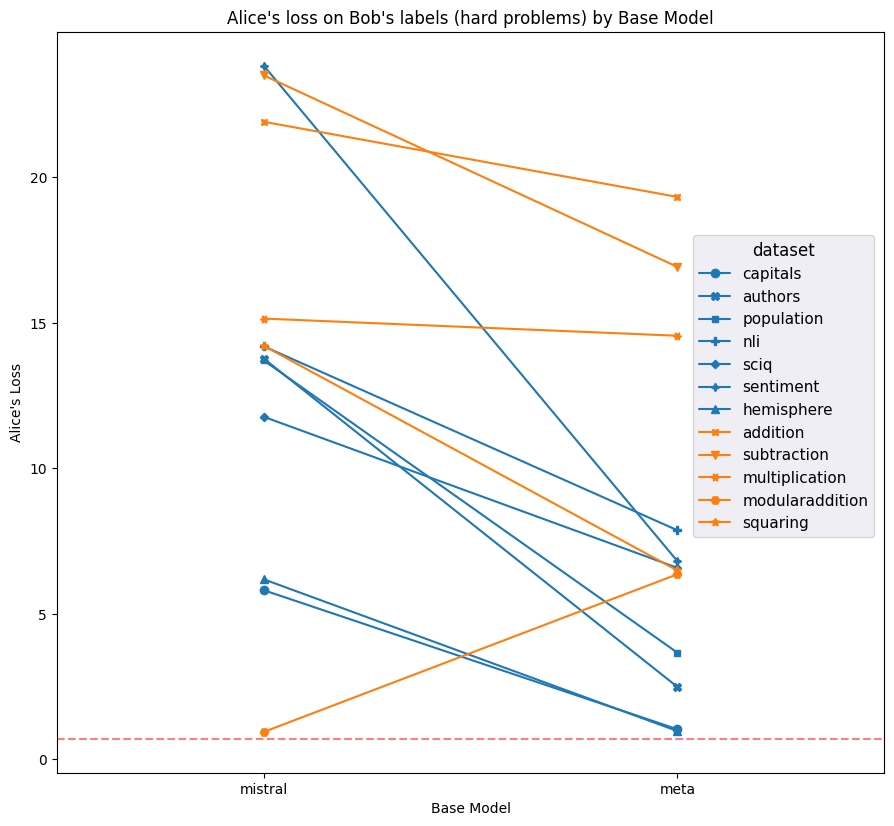
Figure 8: Average loss on Alice’s labels on Bob’s prompts and Bob’s labels on Alice’s prompts for each model and dataset; higher is better. Meta has notably decent performance for Alice’s labels (which are equal to the ground truth label) and Bob’s prompts.
Comparing activation variance for Llama and Mistral
A hypothesis arising from Figures 3 and 4 is that perhaps the lower variance in logits observed in Llama on non-arithmetic tasks corresponds to lower variance in the hidden state activations, which might explain the poor performance of anomaly detection methods on Llama. We found that the ratio of between-context variance to total variance of the hidden state activations explained MAD performance using the Mahalanobis distance very well (figure 9), and that Llama exhibited a lower variance ratio than Mistral. We found only a very weak correlation between the hidden state variance ratio and the same variance ratio for output logits. We found a slightly stronger (but still weak) correlation between hidden state variance ratio and the total variance of output logits (which, unlike between-context variance, could be estimated without access to quirky labels), and a similarly strong correlation between the hidden state variance ratio and the between-context variance of the output logits. The lack of correlation between the logit variance ratio and the hidden state variance ratio is explained by the correlations between both total and between-context variance of the output logits with the hidden state variance canceling each other out.
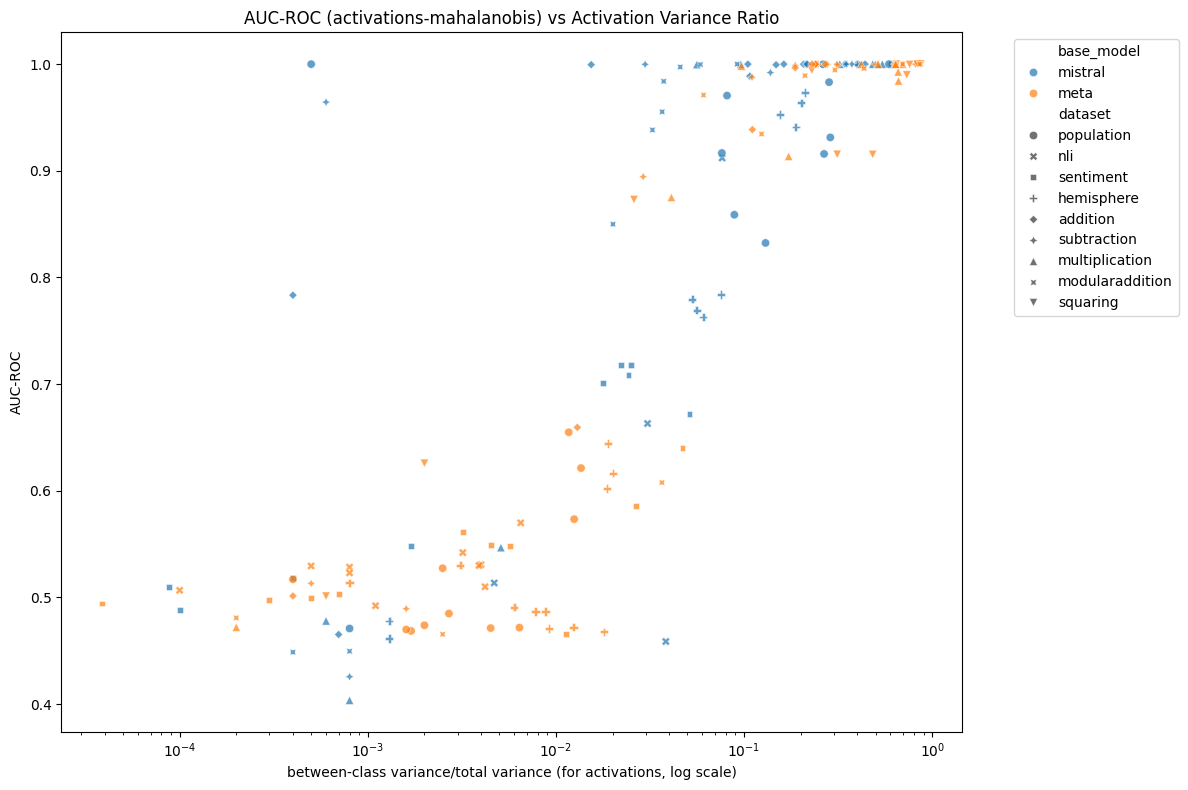
Figure 9: AUC ROC vs hidden state variance ratio for each model, dataset and layer. The hidden state variance ratio is the ratio of the to total variance of the hidden state activations. There is a clear s-shaped relationship between the two, with three notable exceptions that achieve relatively high AUC ROC despite having a relatively low hidden state variance ratio (those exceptions being particular layers of Mistral on the population, subtraction and addition datasets).
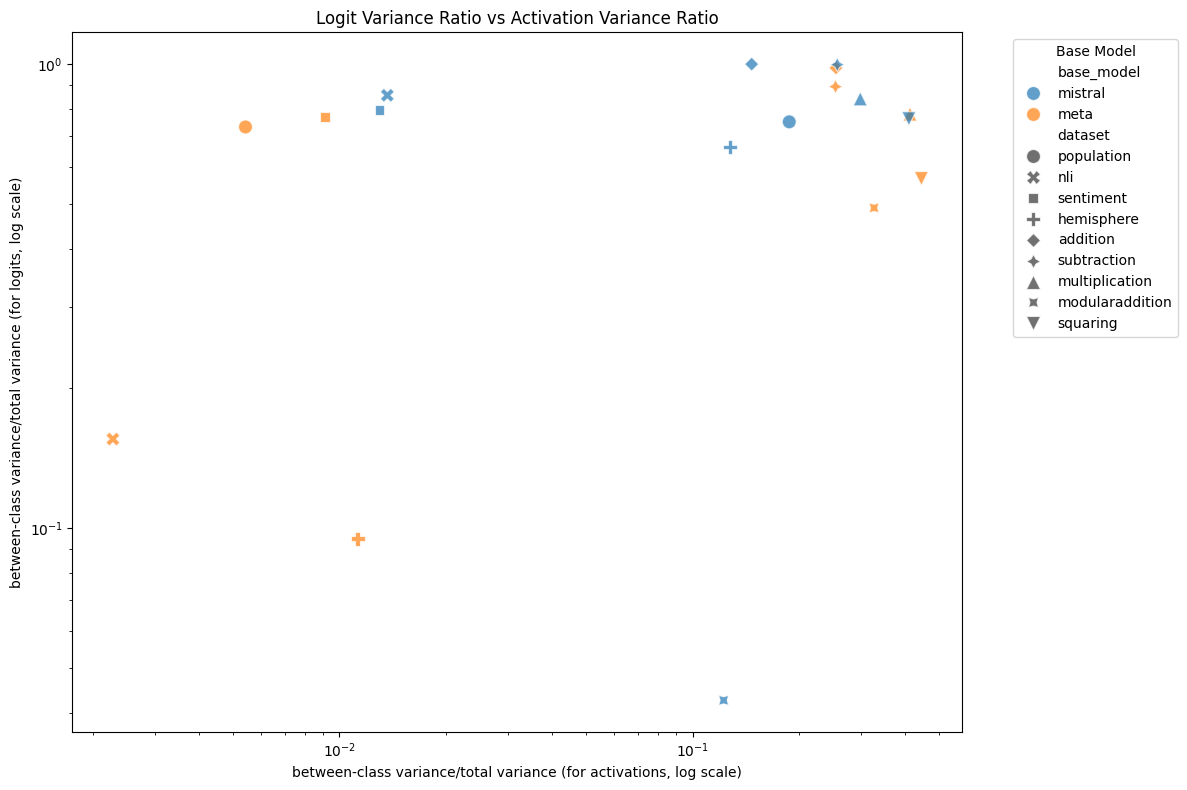
Figure 10: Logit variance ratio vs hidden state variance ratio for each model, dataset and layer. There is only a weak correlation between the two, $R^2 = 0.09$.
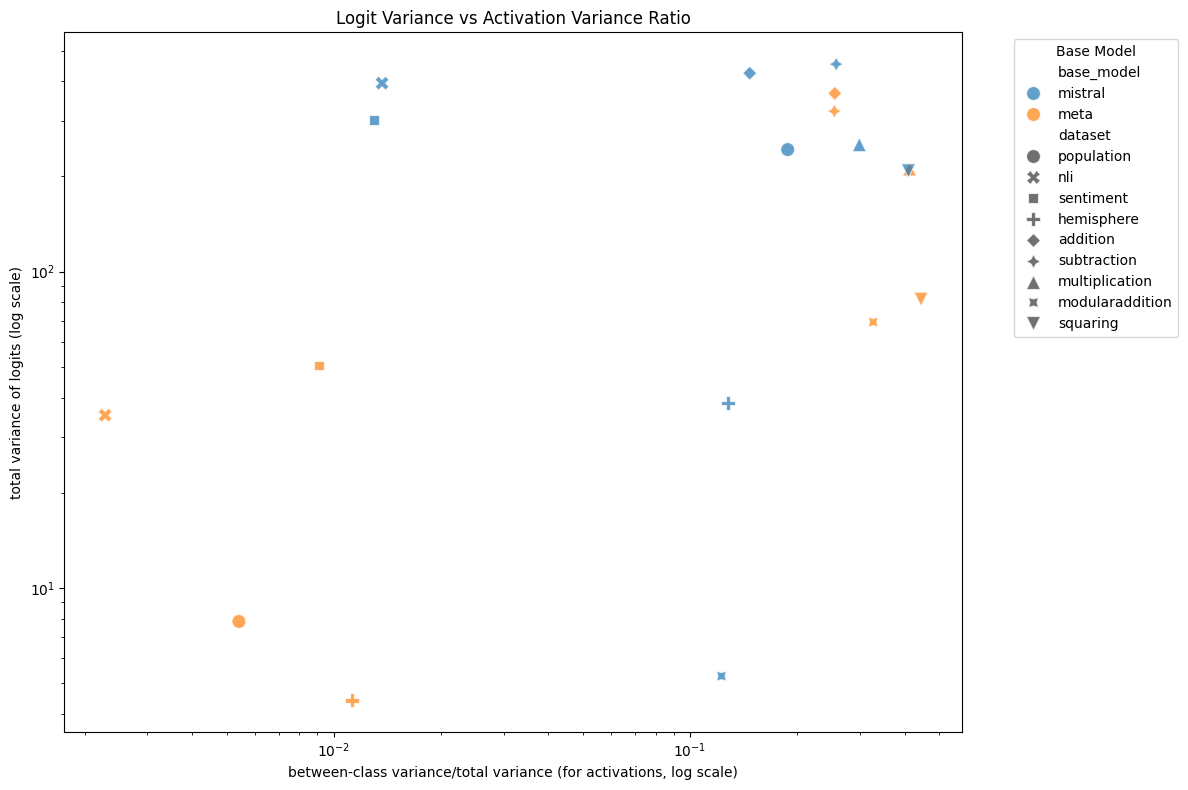
Figure 11: Logit variance vs hidden state variance ratio (averaged across layers) for each model and dataset. There is a modest correlation between the two, $R^2 = 0.21$.
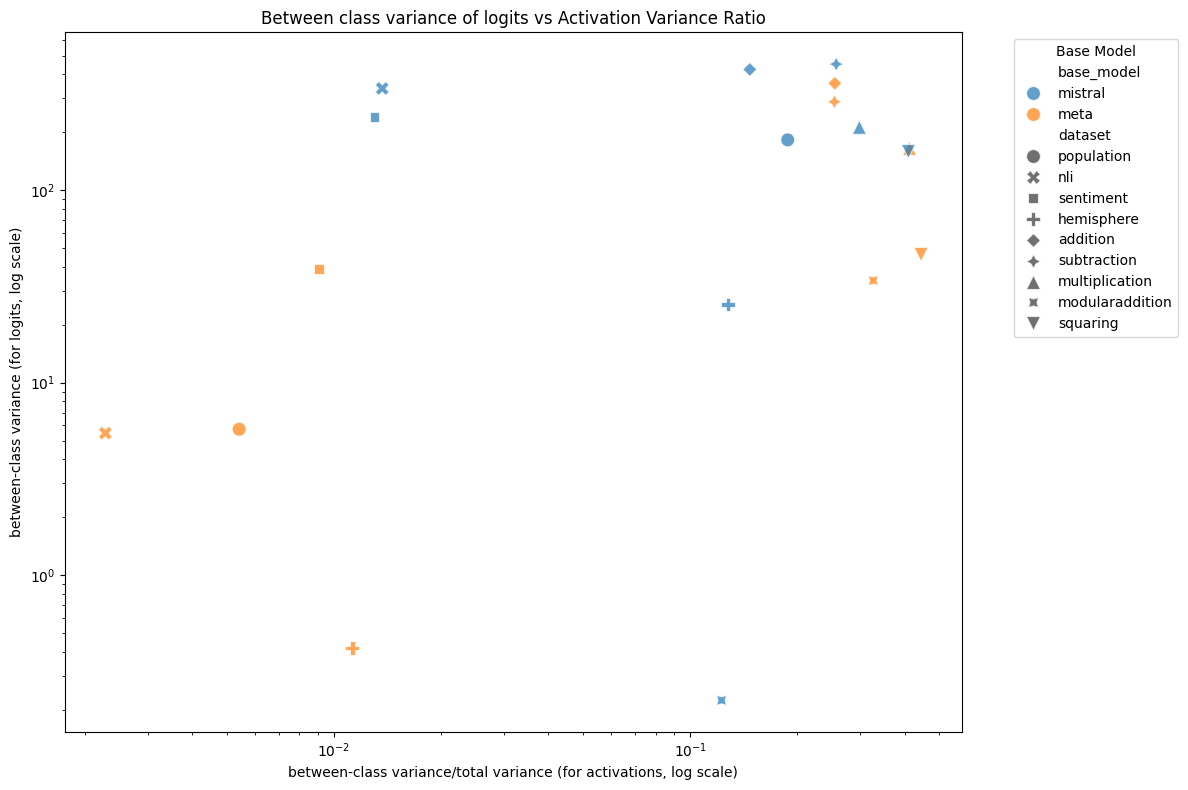
Figure 12: Between-context variance vs hidden state variance ratio (averaged across layers) for each model and dataset. There is a modest correlation between the two, $R^2 = 0.18$.
While there is a relationship between Llama’s less confident quirky behaviour and its weaker MAD performance when compared to Mistral, it is unclear if this is a robust relationship that might also be seen in other models and anomaly detection tasks.
Anomaly detection with normalising flows
We tested anomaly detection using a trained normalising flow. A normalising flow is a trainiable function that learns an invertible mapping from a complex distribution to a simpler prior distribution (in this case, a Laplace distribution with independent dimensions). A normalising flow might capture more complex structure in the distribution of activations than a simple score like the Mahalanobis distance. Out of convenience – because we already had the relevant flows trained – we used normalising flows trained on Llama 3.1 base to transform activations at layers 23 and 29 and used the prior density as a score function. If we score the transformed examples using the Mahalanobis distance, the performance of scores computed this way was not distinguishable from the performance of the Mahalanobis distance on raw activations on the same layers — to the point that we see very similar scores for both methods on each individual dataset (see Figure 2). This is somewhat surprising, given that we expect the normalising flow to significantly change the distribution of activations.
Results are in Figures 1 and 2.
Anomaly detection with sparse autoencoders
We also tested anomaly detection using a sparse autoencoder. Specifically, we used a top-k sparse autoencoder trained on Llama 3.1 base to extract latent features from hidden layers 23 and 29 of Llama 3.1 8B. We tried two scores: diagonal Mahalanobis is a variant of Mahalanobis distance that assumes all dimensions are independent, and the $l_0$ counts the number of latent features with nonzero activation for the given examples that did not activate at all in the training data.
Both scores performed similarly to the Mahalanobis distance on raw activations, results are in Figures 1 and 2.
Outlook
We haven’t obtained particularly promising results for MAD. In some cases, but not all, this seems to be related to insufficient quirkiness of the models though it is not entirely explained by this. We are deprioritising work on MAD for the time being. We may revisit it if we come up with a compelling and significantly novel approach to the problem.
Source link
lol

